Le mixage audio
29 Jan 2013Que se passe-t-il lorsque nous percevons le son provenant de plusieurs sources audio simultanément, par exemple lorsque plusieurs personnes parlent en même temps ?
Dans la réalité, ce que nous entendons est la somme de chacun des signaux.
Mais si nous voulons mélanger plusieurs pistes audio numériques, nous
rencontrons un problème : chaque échantillon d’un signal audio est compris
entre une valeur min et une valeur max, disons entre -1 et 1. Pour les
mixer, nous ne pouvons donc pas sommer plusieurs signaux comme dans la
réalité : le signal résultant doit aussi être compris entre -1 et 1. Comment
faire alors ?
En théorie
Les graphes présentés dans les sections suivantes ont été créés avec
gnuplot, et les définitions de fonctions sont écrites dans la syntaxe
correspondante. Les sources (.gnu) sont disponibles pour chacun des graphes,
vous permettant de les manipuler en 3D.
Somme tronquée
La première idée est de sommer les signaux en tronquant le résultat dans
l’intervalle [-1; 1]. Pour le mixage de deux sources audio x et y :
mix_sum(x, y) = min(1, max(-1, x + y))Le résultat sera parfait lorsque |x + y| <= 1. Par contre, dans le reste des
cas, nous obtenons du clipping, désagréable à l’oreille.
Visualisons cette fonction :
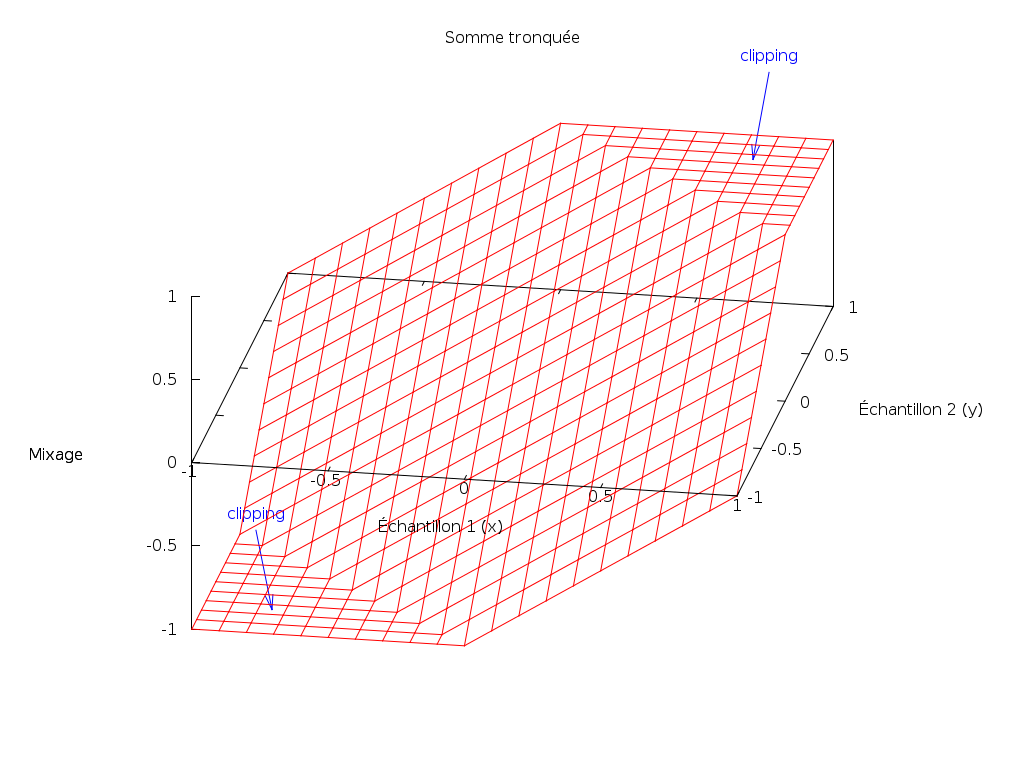
Les axes horizontaux correspondent à un échantillon de chacune des deux sources audio ; l’axe vertical représente la valeur résultant de la combinaison des deux en utilisant la somme tronquée.
Le clipping correspond aux deux paliers horizontaux du haut et du bas.
Moyenne
Pour éviter tout clipping, il suffirait de moyenner les deux sources audio :
mix_mean(x, y) = (x + y) / 2;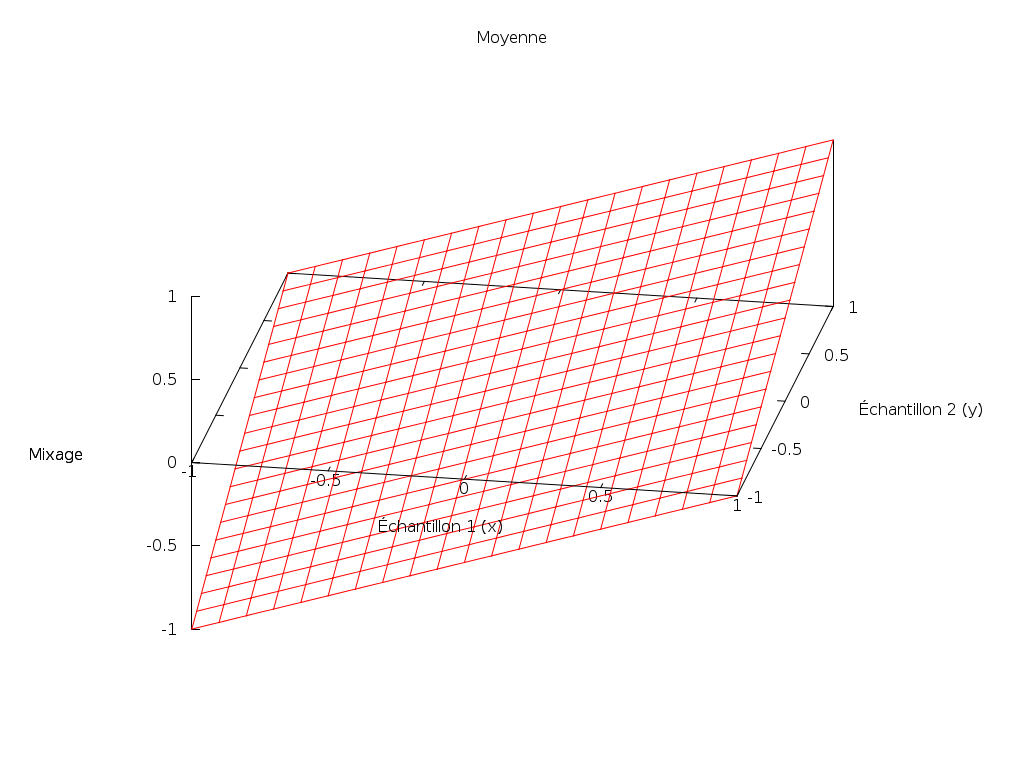
Effectivement, ça fonctionne bien. Mais ce n’est pas forcément le meilleur choix.
Le son résultant va toujours être plus faible que le plus fort des deux sources, et souvent de manière significative. En particulier, si nous mélangeons une source audio quelconque avec un silence, l’amplitude va être divisée par deux.
De plus, la définition va également être divisée par deux : si l’amplitude est codée sur 8 bits, elle peut prendre 256 valeurs. En divisant les signaux par deux, chaque signal aura une définition de 7 bits (128 valeurs).
Ces inconvénients s’agravent lorsqu’il y a plus de deux sources à mélanger.
k × somme
Nous pouvons alors chercher un compromis entre conserver l’amplitude et éviter le clipping. En fait, les fonctions de somme tronquée et de moyenne ne sont que deux cas particuliers de cette fonction :
mix_ksum(k, x, y) = min(1, max(-1, k * (x + y)))En effet :
mix_sum(x, y) = mix_ksum(1, x, y)
mix_mean(x, y) = mix_ksum(0.5, x, y)Nous pouvons choisir n’importe quel k entre 0.5 et 1 : plus k est faible,
moins le clipping sera probable ; plus k est élevé, plus l’amplitude sera
conservée.
Voici le graphe pour k = 0.7 :
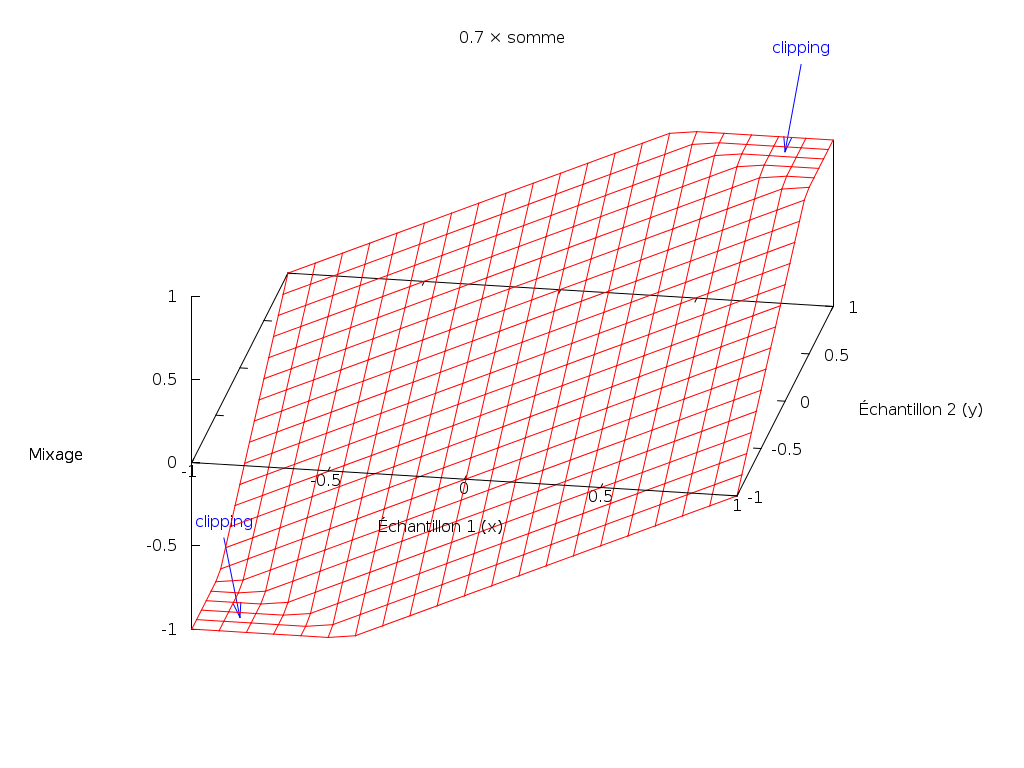
Cette méthode est très utile si nous connaissons à l’avance les sources audio.
Par exemple, pour mélanger deux fichiers son, nous pouvons effectuer une
première passe pour analyser le max m de la somme des deux signaux, et choisir
k < 1/m : cela garantit qu’il n’y aura pas de clipping, et nous pouvons
conserver l’amplitude dans la mesure du possible, sans distorsion.
Si ces sources audio nous parviennent en direct (streaming, conversation
audio…), nous pouvons choisir un nombre arbitrairement (plus ou moins basé sur
l’expérience). Choisir k > 0.5 se justifie car si deux sources audio sont
indépendantes, les ajouter ne provoque pas des pics deux fois plus importants
(les pics d’un signal vont souvent être compensés par les creux de l’autre).
Fonction non-linéaire
Mais nous pouvons trouver un meilleur compromis grâce à des fonctions non-linéaires.
Dans la première partie de son billet Mixing digital audio, Viktor T. Toth présente une stratégie très intéressante. Il part du principe que le mixage de deux sources audio doit respecter les règles suivantes :
- si l’une des sources est silencieuse, alors nous voulons entendre l’autre inaltérée ;
- si les signaux sont de même signe, l’amplitude du résultat (en valeur absolue) doit être supérieure à celle des sources.
Et si les signaux prennent valeur dans [0, 1], la fonction suivante respecte
ces contraintes :
vtt(x, y) = x + y - x * y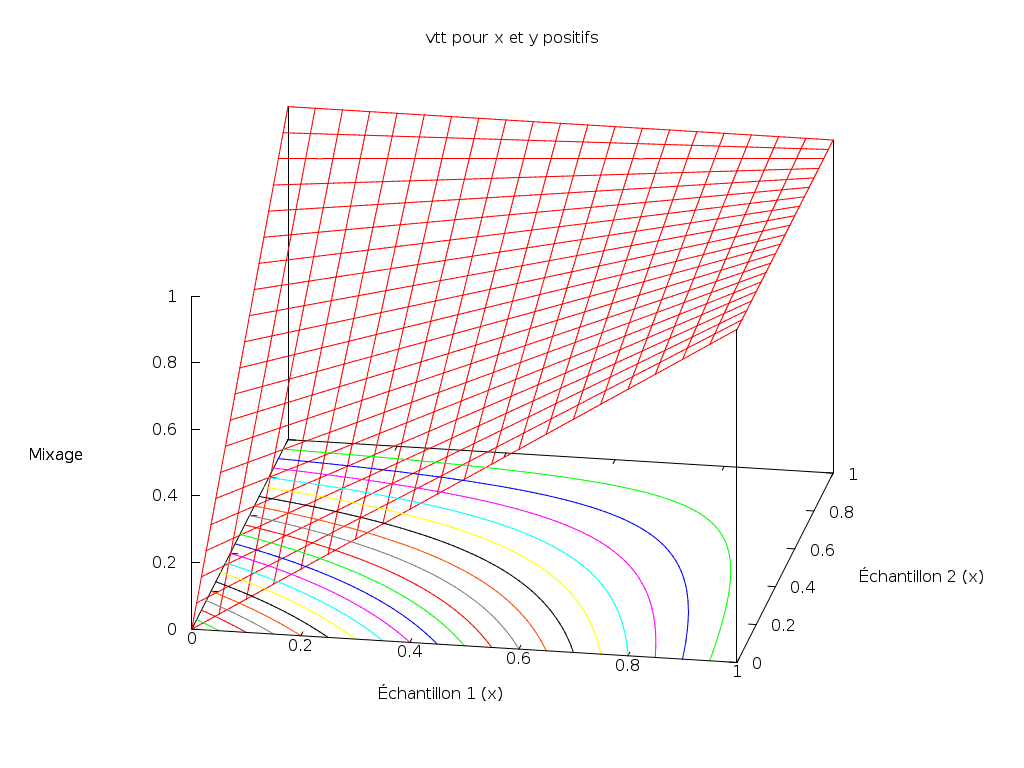
Cependant, en réalité, les signaux prennent valeur dans [-1, 1], et cette
fonction ne convient pas. L’auteur s’en est rendu compte, mais malheureusement
la solution qu’il propose n’est pas appropriée (par exemple, le mixage ne se
comporte pas symétriquement si nous inversons le signal).
Nous pouvons extrapoler son idée originale pour la faire fonctionner sur [-1,
1] :
mix_vtt(x, y) = \
x >= 0 && y >= 0 ? x + y - x * y \
: x <= 0 && y <= 0 ? x + y + x * y \
: x + yLe principe est d’utiliser le symétrique de sa fonction pour la partie négative, et ajouter deux bouts de plans pour les raccords :
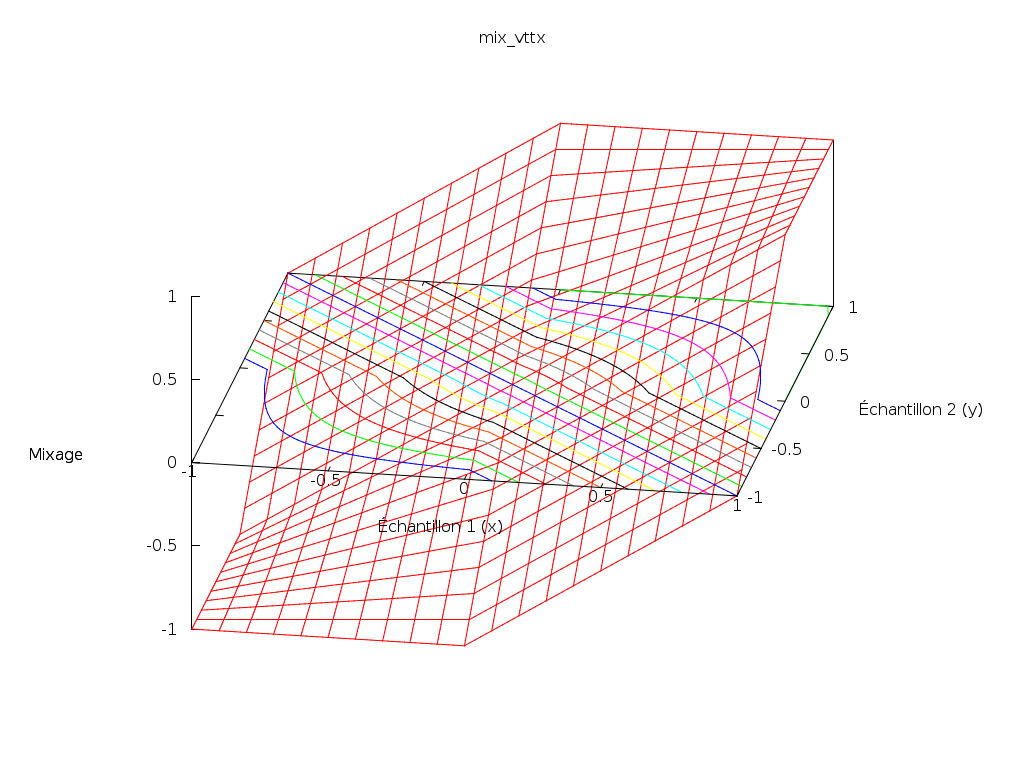
Mais quelque chose saute aux yeux : sa représentation n’est pas lisse (la fonction n’est pas continûment dérivable (C1)). Cela signifie que les variations du résultat en fonction des variations des sources changent brutalement en certains endroits.
Ce n’est pas satisfaisant mathématiquement.
Surface lisse
Et en effet, en y réfléchissant, la fonction souffre de quelques défauts.
Par exemple, si l’une des deux sources audio est à 1, alors si l’autre est
positive, elle n’a aucun impact, si elle est négative, elle a un impact
linéaire important. Ce n’est rien d’autre qu’un clipping de l’une des deux
sources.
Par ailleurs, dans la réalité, le mixage de deux signaux est simplement leur addition. Le résultat devrait donc être invariant si nous ajoutons une constante à une source et la soustrayons à l’autre :
mix(x, y) = mix(x + k, y - k) = x + yCette propriété me semble importante : peu importe que le son provienne d’une source ou d’une autre, cela n’intervient pas dans le mixage.
Or, dans la fonction précédente, elle n’est pas respectée. Par exemple :
mix_vttx(0.5, 0.5) = 0.75
min_vttx(0, 1) = 1Afin de dépasser ce problème, posons cette propriété comme principe : puisque
l’identification de l’apport individuel de chaque signal ne compte pas,
considérons uniquement leur somme (ou leur moyenne). Ainsi, au lieu d’une
fonction à deux variables x et y, nous pouvons utiliser une fonction à une
seule variable z = (x + y) / 2 (la moyenne).
Remarquons que nous pouvions déjà exprimer les fonctions linéaires vues
précédemment en fonction d’une seule variable. En effet, en posant z = (x + y)
/ 2, nous obtenons :
sum(z) = max(-1, min(1, 2 * z))
mean(z) = z
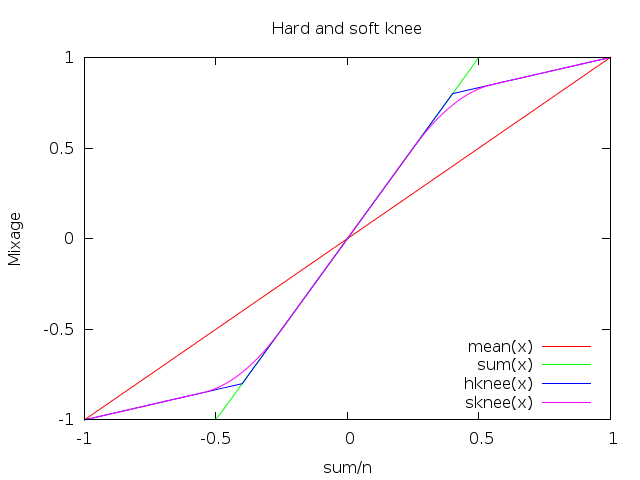
ksum(z) = max(-1, min(1, 2 * k * z))Dans le fond, nous cherchons une fonction qui s’approche de sum pour les
amplitudes faibles (pour conserver l’amplitude au mieux) et de mean pour les
amplitudes élevées (pour éviter le clipping).
Avec un peu d’imagination, nous pouvons trouver une fonction qui convient parfaitement (pour 2 pistes audio) :
g(z) = z * (2 - abs(z))Elle se généralise pour n pistes audio :
g(z) = sgn(z) * (1 - (1 - abs(z)) ** n)abs(x) désigne la valeur absolue de x (|x|), et ** est la fonction
puissance (a ** n signifie an)
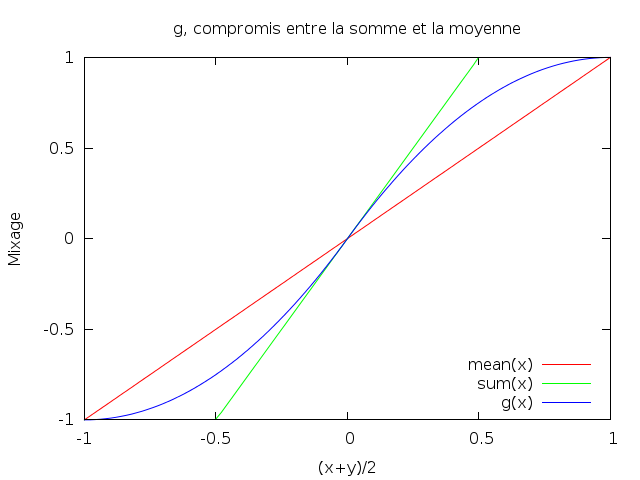
Cette fonction a plein de propriétés intéressantes :
- ∀x, |g(x)| <= 1
- dans le bon intervalle
- g(-1) = -1, g(0) = 0 et g(1) = 1
- résultats cohérents
- ∀x (|x| < 1), g’(x) > 0
- pas de clipping
- ∀x, |g(x)| ≤ |sum(x)|
- l’amplitude ne dépasse jamais la somme de celle des sources
- ∀x, |g(x)| ≥ |mean(x)|
- l’amplitude est toujours supérieure à la moyenne des sources
- ∀x, g’(0) = sum’(x) = n
- g se comporte comme sum lorsque l’amplitude est faible (elle varie de la même manière)
- ∀x≠0, x.g’‘(x) < 0
- la croissance de g ralentit lorsque l’amplitude augmente (en valeur absolue), donc les fortes amplitudes sont plus compressées que les faibles
- ∀x, g(-x) = -g(x) (impaire)
- comportement symétrique sur un signal inversé
- g ∈ C1 (continûment dérivable)
- parfaitement lisse
Passons alors en 3 dimensions, et posons :
mix_f(x, y) = g((x + y) / 2)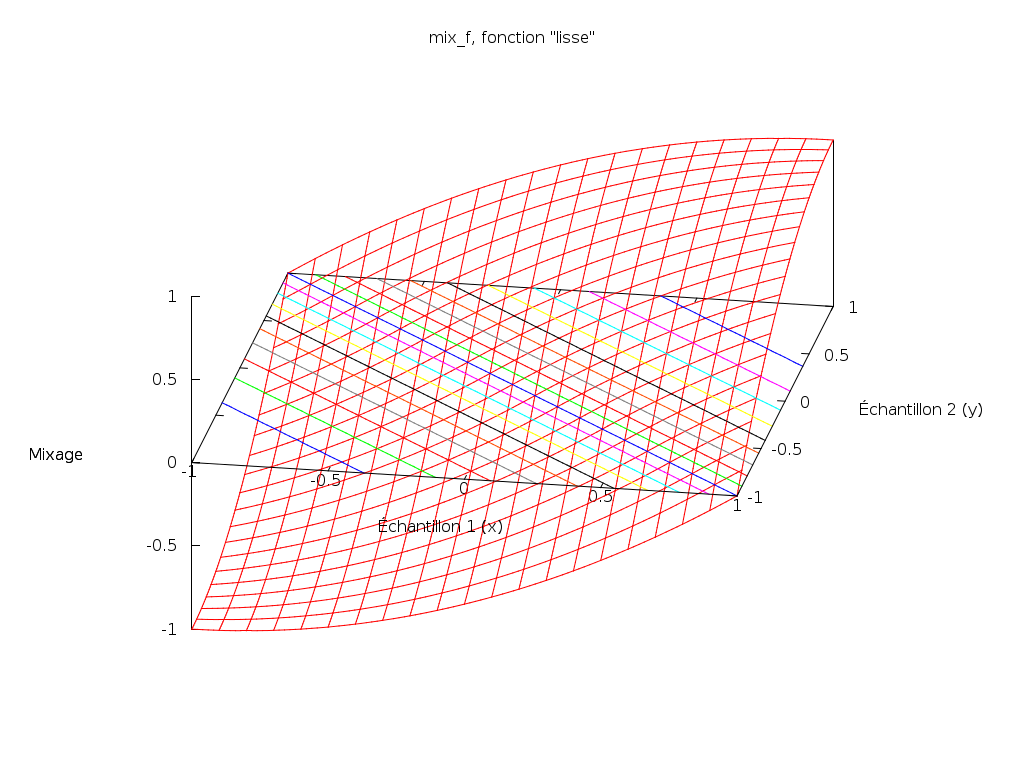
Nous nous apercevons que c’est une version lissée de la fonction précédente :
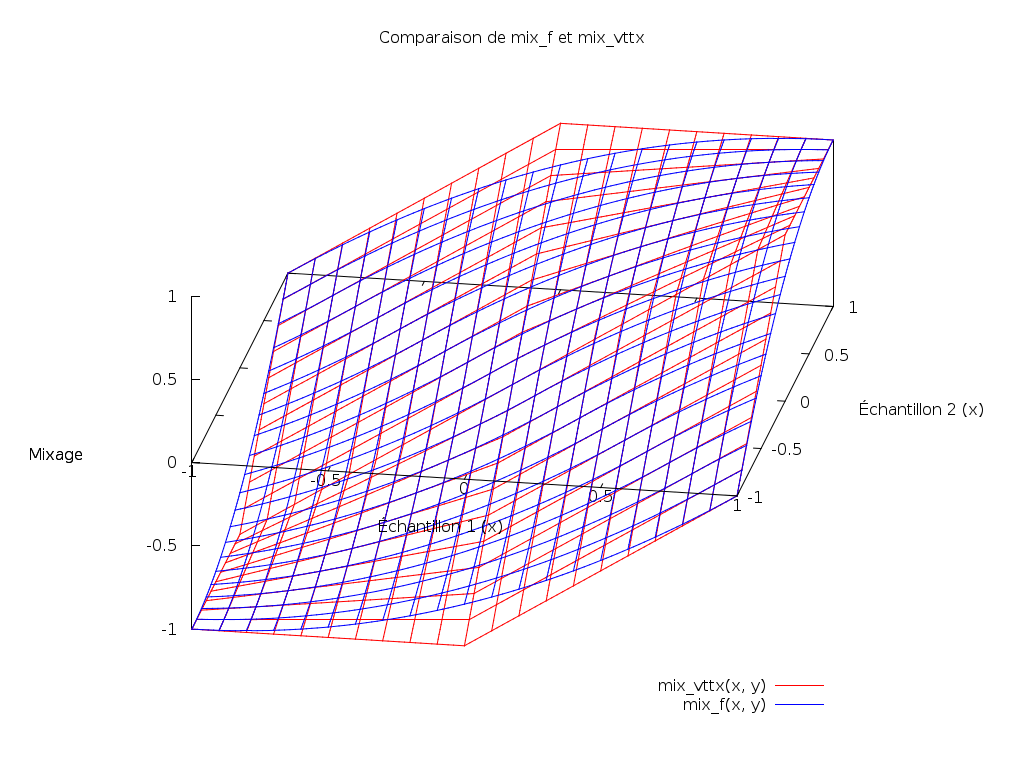
Cette fonction me semble donc pertinente pour mixer plusieurs flux audio.
En pratique
Bon, jusqu’ici nous avons fait de beaux dessins, c’était rigolo. Maintenant, passons à la pratique, et implémentons les fonctions de mixage en C.
Nous manipulerons uniquement des flux audio brut (des wav sans en-tête), contenant uniquement des échantillons encodés par des entiers signés sur 16 bits, en little endian. Ça peut paraître compliqué comme ça, mais c’est juste le format utilisé pour les cd audio.
Le programme est indifférent au nombre de canaux ou à la fréquence (il mixe les échantillons les uns à la suite des autres), mais bien évidemment les différentes pistes mixées doivent avoir ces paramètres identiques.
Implémentation
Bien que nous n’ayons vu jusqu’ici que le mixage de deux pistes audio (au-delà c’était compliqué de les visualiser sur des graphes), l’implémentation permet de mixer n pistes audio.
Le mixage s’effectue sur un échantillon de chaque piste audio à la fois (il est indépendant des échantillons précédents et suivants). Les fonctions de mixage ont toutes la même signature :
int mix(int n, int samples[]);n- le nombre de pistes audio
samples- le tableau des
néchantillons à mixer
La valeur du retour ainsi que celles des samples[i] tient sur 16 bits (compris entre -32768 et 32767).
À titre d’exemple, voici l’implémentation de la fonction f (celle qui est lisse) :
int mix_f(int n, int samples[]) {
double z = _dsum(n, samples) / n;
int sgn = z >= 0 ? 1 : -1;
double g = sgn * (1 - pow(1 - sgn * z, n));
return to_int16(g);
}avec _dsum une fonction qui somme les n samples et to_int16 une fonction
qui convertit un flottant compris entre -1 et 1 vers un entier compris entre
-32768 et 32767.
Une fonction main s’occupe d’ouvrir les fichiers dont les noms sont passés en
paramètres et d’appliquer pour chaque échantillon la fonction de mixage
désirée.
Sources
Les sources complètes sont gittées : mixpoc.
Le projet contient :
- le code du PoC (
mixpoc.c) ; - un makefile minimaliste (
Makefile) ; - les sources des graphes gnuplot (
*.gnu) ; - des scripts utilitaires (voir ci-dessous l’utilisation).
Utilisation
Fichiers raw
Le PoC ne manipule que des fichiers raw. Il est peu probable que vous ayez de tels fichiers sur votre ordinateurs, vous devez donc pouvoir en créer à partir de vos fichiers audio habituels.
Vous aurez besoin de sox et éventuellement avconv ou ffmpeg.
./toraw file.wav file.raw
./toraw file.ogg file.raw
./toraw file.flac file.raw
Pour l’opération inverse :
./rawtowav file.raw file.wav
Si le format n’est pas supporté par sox (comme le mp3), convertissez-le en
wav d’abord :
avconv -i file.mp3 file.wav
ffmpeg -i file.mp3 file.wav
Lecture et enregistrement
Il est possible de lire des fichiers raw directement et d’en enregistrer de nouveaux à partir du microphone (pratique pour essayer de mixer une musique avec une conversation).
Le paquet alsa-utils doit être installé (vérifiez que le microphone est bien
activé dans alsamixer).
Pour enregistrer :
./record file.raw
./record > file.raw
Pour lire :
./play file.raw
./play < file.raw
Pour lire en direct le son provenant du microphone (à tester avec un casque pour éviter l’effet Larsen) :
./record | ./play
Mixpoc
Pour compiler mixpoc (nécessite make et un compilateur C comme gcc) :
make
Pour l’utiliser, la syntaxe est la suivante :
./mixpoc (sum|mean|ksum|vttx|f) file1 [file2 [...]]
Le résultat sort sur la sortie standard. Ainsi :
./mixpoc f file1.raw file2.raw filen.raw > result.raw
écrit le fichier result.raw.
Pour lire en direct le résultat :
./mixpoc f file1.raw file2.raw filen.raw | ./play
ou plus simplement (grâce au script mix) :
./mix f file1.raw file2.raw filen.raw
Pour ajouter une source silencieuse, vous pouvez utiliser /dev/zero :
./mix f file.raw /dev/zero
Vous avez maintenant tout ce dont vous avez besoin pour tester.
Gnuplot
Pour visualiser les graphes gnuplot, je vous conseille le paquet gnuplot-qt.
Pour les ouvrir :
gnuplot -p file.gnu
La souris ou les flèches du clavier permettent de tourner le graphe en 3 dimensions.
Les commandes nécessaires pour générer une image .png sont écrites en
commentaire à l’intérieur du fichier. Je les ai fait commencer par ## pour
pouvoir les décommenter automatiquement (sans décommenter le reste) avec un
script.
Ainsi, pour générer les fichiers .png :
./gg file.gnu
./gg *.gnu
Conclusion
Pour mixer plusieurs pistes son, la fonction f me semble très bonne, à la fois en théorie et en pratique. Sur les exemples que j’ai testés, le résultat était celui attendu.
Cependant, je n’ai ni du matériel audio ni des oreilles de haute qualité, et mes connaissances en acoustique sont très limitées.
Les critiques sont donc les bienvenues.
J’ai bien l’impression que tu as construit un compresseur :)
http://fr.wikipedia.org/wiki/Compresseur_%28audio%29